Wolmer’s Trust High School for Girls
CAPE COMPUTER SCIENCE
Grades: Upper and Lower Six Teacher: Mrs. McCallum-Rodney
STANDARD ABSTRACT DATA TYPES – STACKS
DEFINITION:
A stack is a homogeneous collection of items of any one type, arranged linearly with access at one end only - called the top. This means that data can be added or removed from only the top. Formally this type of stack is called a Last In, First Out (LIFO) stack. Data is added to the stack using the Push operation, and removed using the Pop operation.
DESCRIPTION:
In order to clarify the idea of a stack let's look at a "real life" example of a stack. Think of a stack of plates in a high school cafeteria. When the plates are being stacked, they are added one on top of each other. It doesn't make much sense to put each plate on the bottom of the pile, as that would be far more work, and would accomplish nothing over stacking them on top of each other. Similarly, when a plate is taken, it is usually taken from the top of the stack.
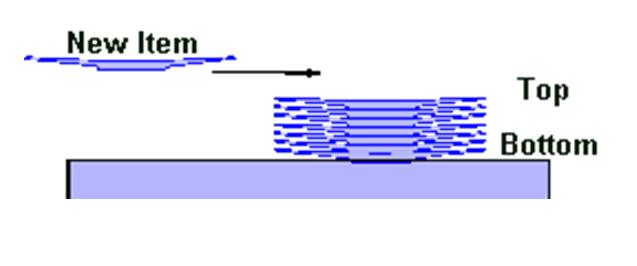
STACK IMPLEMENTED AS AN ARRAY
One of two ways to implement a stack is by using a one dimensional array (also known as a vector). When implemented this way, the data is simply stored in the array. Top is an integer value, which contains the array index for the top of the stack. Each time data is added or removed, top is incremented or decremented accordingly, to keep track of the current top of the stack. By convention, an empty stack is indicated by setting top to be equal to -1. 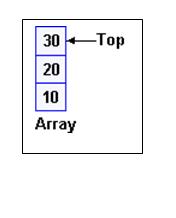
Stacks implemented as arrays are useful if a fixed amount of data is to be used. However, if the amount of data is not a fixed size or the amount of the data fluctuates widely during the stack's life time, then an array is a poor choice for implementing a stack. For example, consider a call stack for a recursive procedure. First, it can be difficult to know how many times a recursive procedure will be called, making it difficult to decide upon array bounds. Second, it is possible for the recursive procedure to sometimes be called a small number of times, called a large number of times at other times. An array would be a poor choice, as you would have to declare it to be large enough that there is no danger of it running out of storage space when the procedure recurses many times. This can waste a significant amount of memory if the procedure normally only recurses a few times.
STACK IMPLEMENTED AS A Linked List
To solve the problems discussed in the last section, a stack can be implemented using pointers, as a form of a linked list. When a stack is implemented this way, each node contains a data field for the information, and a pointer to the next node on the list. Top is a pointer to the top of the list. When top is NULL (or NIL, depending on the programming language), the stack is empty. Implementing stacks as linked lists provides a solution to the problem of dynamically growing stacks, as a linked list is a dynamic data structure. The stack can grow or shrink as the program demands it to. However, if a small and/or fixed amount of data is being dealt with, it is often simpler to implement the stack as an array.
OPERATIONS ON STACKS
Now that you know what a stack is we will now discuss some operation that can be performed on a stack.
Remember, a stack has a maximum size of n.
|
Operation |
Description |
Requirement |
|
Push |
This operation adds or pushes another item onto the stack. |
The number of items on the stack is less than n. |
|
Pop: |
This operation removes an item from the stack. |
The number of items on the stack must be greater than 0. |
|
Top: |
This operation returns the value of the item at the top of the stack. |
Note: It does not remove that item. |
|
Is Empty: |
This operation returns true if the stack is empty and false if it is not. |
|
|
Is Full: |
This operation returns true if the stack is full and false if it is not. |
|
OPERATION - PUSH
Push is the function used to add data items to the stack.
In order to understand how the Push function operates, we need to look at the algorithm in more detail.
procedure Push( item, stack)
{top is the current top of stack and n is its maximum size}
MODULE NAME : Push
INPUT : item, stack[n], n
OUTPUT : None
PROCESS :
IF top == n-1 THEN
PRINT “stack is full”
ELSE
top = top + 1
stack[top] = item
ENDIF
ENDMODULE
OPERATION - POP
Data is removed from a stack by using Pop. From a procedural perspective, pop is called with the line Pop(item), where item is the variable to store the popped item in. Pop returns the item at the top of the stack (and only that item).
Once again, we will begin by looking at the algorithm.
MODULE NAME : Pop
INPUT : None
OUTPUT : item
PROCESS :
{remove top element from the stack and put it in the item}
IF top = -1 THEN
PRINT “stack is empty”
ELSE
item = stack[top]
top = top-1;
ENDIF
ENDMODULE
OPERATION - TOP
What if you want to access the data field at the top of the stack, but you do not want to remove the item? It seems like a hassle (not to mention that it is inefficient) to pop the top item, use it, and push it back onto the stack. The solution to this problem is the function Top (do not confuse this function with the variable top). Top will return the data segment of the top item without removing it from the stack. It is called with Top(item), where item is a variable that will hold the data item.
As usual, we will start by looking at the algorithm.
Module Name : TOP
Input : stack [n], n, top
Output : item
Process :
{return top element from the stack stack and put it in the item}
IF top == -1 THEN
PRINT “ stack is empty”
ELSE
item = stack[top]
RETURN item
ENDIF
EndModule
OPERATIONS - IS_EMPTY AND IS_FULL
Þ Is_Empty
Is_Empty is a function that will tell you if the stack is empty. Is_Empty is implemented as follows:
Module Name : Is_Full
Input : n, top
Output : True/False
Process :
RETURN top == -1
EndModule
Is_empty will return a value (normally a boolean value) that will tell you if the stack is empty or not.
Þ Is_Full
Is_Full is a function that will tell you if a stack is full. First, there must be number n defined, which is the maximum number of elements allowed in the stack. For array implementation's, it is simpler if n is defined as (Maximum size - 1), due to the fact that the array indexing starts at -1 for an empty stack. Is_Full is implemented as follows:
Input : n, top
Output : True/False
Process :
RETURN top == n-1
EndModule
SIZE
Checking the size of the stack is a fairly simple task. If you are implementing the stack as an array, the size of the stack will be
(top + 1)
The 1 is added because top is initially -1, when the stack is empty, or size equals 0.
If you are implementing the stack as a linked list, you must keep a counter that will keep track of the number of items in the stack. This counter is initially set to zero, when the stack is empty. Each time an item is added, the counter is incremented, and each time an item is popped, the counter is decremented. At any given time, the size of the stack will be the value of this counter.
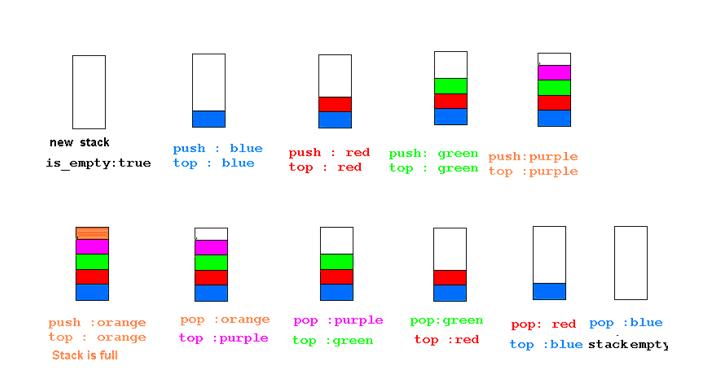
PICTORIAL OVERVIEW
The following is a detailed example of the procedures we have discussed on an array implementation of a stack.
STACK APPLET
http://www.cs.usask.ca/resources/tutorials/csconcepts/1998_5/stacks/java/index.html