Queues

 

Wolmer’s Trust High School for Girls

CAPE COMPUTER SCIENCE 

Grades:  Upper and Lower Six                   Teacher:  Mrs. McCallum-Rodney 

 DEFINITION

A queue is an ordered homogeneous group of items in which the items are added at one end (the back) and are removed from the other end (the front). This is known as a First In, First Out (FIFO) data structure.

DESCRIPTION

Queues in computer science are very similar to queues in real life. A queue in real life would be a line up at a fast food counter or a bank teller. The people are dealt with in the order that they arrived.

In computer science this is called FIFO (first in-first out) queue. Items can only be removed from the queue in the order that they are inserted into it.

Queues are very common in the everyday functions of computers. The most obvious is printing queues. When you send multiple print jobs to a printer, each printing job is inserted at the rear of the queue in the order it was sent. Each job is then printed in the order sent to the printer. Any type of stream throughout I/O will use a queue. Processes waiting to be executed by a CPU are usually in form of a queue also. Although these may take the form of a priority queue.

THE QUEUES IMPLEMENTED AS AN ARRAY

An array based implementation of a queue, as stated before, involves declaring an array of some size, then simply adding data to the array until it is full.

If a Dequeue operation is performed on any element beside the last one, then we would need to move every element in the queue up one slot. This design is very simple but it has some drawbacks. The major drawback in this design is the fact that you must move all the elements forward in the queue whenever a Dequeue operation is performed. This is so the entire queue can be used. Otherwise we would rapidly run out of queue, even though there is space!

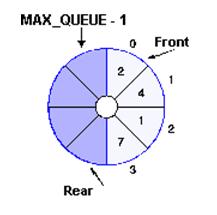
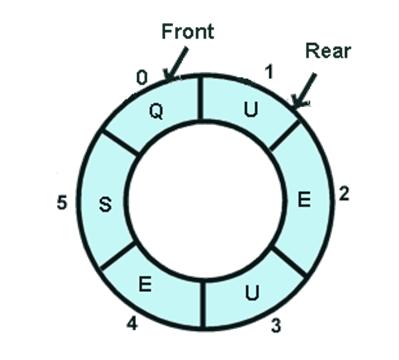
 When data is removed or dequeued from the array, the data comes out in the same order in which it was inserted. The easiest way to picture this happening is to think of the array as circular. Thus in order to remove an item from the queue, the front of the array is accessed. Initially, the first node of the array is defined as the front. Each time an item is removed from the queue the variable front is incremented to point at the next item in the array.

In the example, front is initially pointing to array[0] which has a data value of 2. If we remove an item from the queue the data value is set to null and the front pointer is incremented by one - it now points at array[1]. When the front pointer is pointing at array[MAX_QUEUE - 1] and an item is removed from the queue, the front pointer will now point to array[0] again.

 

THE QUEUE IMPLEMENTED WITH LINKED LIST

The second way of designing Queues is to use linked lists. The main difference between linked lists and arrays is that of flexibility. An array, once declared, is of a fixed size and can not change. Conversely, a linked list is of a variable size. When a new item is added it is simply linked to the end of the queue.

Thus the problem with an array implementation of queues is that it wastes memory if the queue varies in size during its existence. This is because the size of the array will have to be the size of the largest amount of data ever in the queue. Remember we can not extend or reduce the size of the array, so it must account for the largest number initially. This is wasteful especially in instances where the size of data is usually small, but occasionally becomes very large.

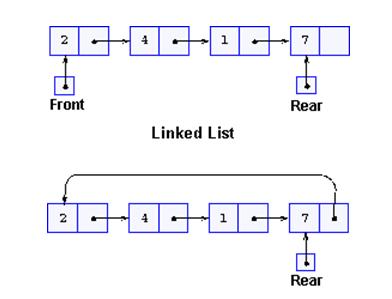
 A linked list implementation of a queue is done by linking together elements to form a chain. In a linked list implementation of a queue the link field of the node will either point to the next node in the queue or to the head of the queue.

Two pointers are needed to mark the front and back of the queue, these are Front and Rear. Without these pointers it would be very easy to loose track of where the queue begins and ends.

 

OPERATIONS ON QUEUES

  

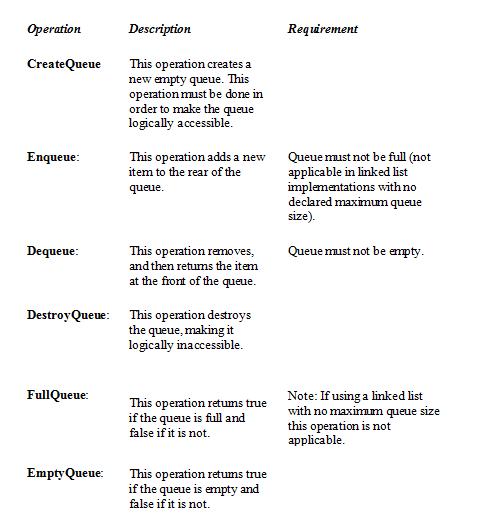
CREATE QUEUES  

CreateQueue is a basic procedure to initialize a queue to an empty state (ie. null). The algorithm is slightly different depending on what type of implementation (Circular Array or Linked List) is chosen, so after the algorithm we will spend some time examining them in detail.

 

Circular Queue

 

 

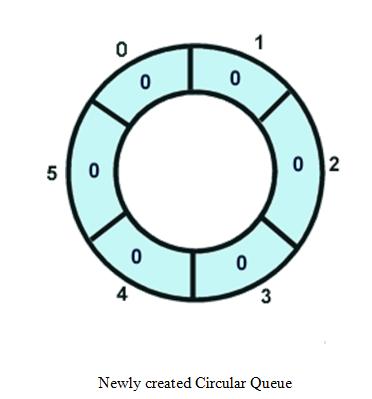
Module Name :           CreateQueue  

Input               :           n, Queue[n],  

Output             :           None 

Process            :          

              

                               DECLARE i AS integer
                             

                               FOR i = 0 TO (n - 1) DO

                                                 Queue[i] = 0\NULL

                               ENDFOR

ENDMODULE

                       

                                        

 

ENQUEUE  

Enqueue is also known as add or insert. It adds new elements to the end of a queue - just like when a person walks up to a line in a grocery store.

This section will give algorithm for the Array Implementation of a Queue.

 

Module Name :           Enqueue  

Input               :           n, Queue[n], back, value

Output             :           None

Process            :

                                    IF back == n-1 THEN

                                                PRINT “Queue is Full”

                                    ELSE

                                                back = back +1

                                                Queue[back] = value

                                    ENDIF

EndModule

 

DEQUEUE

 Dequeue is also known as Remove or Serve. It is used when elements are taken off the front of the queue - the person at the grocery till has paid and left

This section will give algorithm for the Array Implementation of Queues.

 

Module Name :           Dequeue  

Input               :           n, Queue[n]  

Output             :           None

Process            : 

                                    DECLARE item, count AS integer

                                    IF back == -1 THEN

                                                PRINT “Queue is empty”

                                               

                                    ELSE

                                                item = Queue[0]

                                               

                                                FOR count = 0 TO back-1

                                                            Queue[count] = Queue[count+1]

                                                ENDFOR

                                               

                                                Queue[back] = 0

                                                back = back - 1                       

                                    ENDIF

ENDMODULE

           

FULLQUEUE

 

FullQueue is a boolean function that returns true if the Queue is full and false otherwise. The Enqueue operation can only be called if the FullQueue operation returns false.

Module Name :           FullQueue

Input               :           size, queue[size], rear

Output             :           True/False

Process            :           RETURN rear == size-1 

Endmodule

  

EMPTY QUEUE

 Dequeue operation can be called only if EmptyQueue returns false.

The procedure's algorithm:

Module Name        :              EmptyQueue

Input                      :              size, Queue[size], rear

Output                   :              True/False

Process                   :              RETURN rear == -1 

EndModule

 

This procedure works in the following manner.

If the front of the queue is -1 then we know the queue is empty. This is because, the rear always points to the last item inserted. It is not incremented unless an item is inserted (in which case it points to that item).

 

Java Applet 

http://www.cs.usask.ca/resources/tutorials/csconcepts/1998_2/queues/java/index.html